作者：孔朝志，付小林，冯永刚

 

　　摘要：介绍了兆瓦级变速变桨距风力发电机组控制算法的实现过程，根据风机的非线性特征，提出了一种通过模型线性化和状态空间方程最小实现整定控制算法参数的方法。再利用MATLAB/Simulink强大的数值计算功能对主要控制环节进行设计及参数调整，并通过BLADED外部控制器模块对完整的控制算法进行了仿真研究。与常规控制算法相比，使用该方法设计的参数在控制过程中同时兼顾到风机的动态特性与稳定性，有效提高机组的运行性能。

 

　　关键词： 风力发电机组； 变速变桨距；控制算法；参数整定；仿真

 

 

　　随着风力发电机组单机容量的不断增大，变速变桨距控制技术已经成为当前风电机组控制的主要方式，利用该技术可以提高捕获风能效率，获得最佳能量输出。风机的运行环境是复杂多变的，对风电机组动态过程的控制，首先需要建立其非稳态气动力模型，然后利用该模型来设计整机控制策略，最后再借助相关软件对风机整个运行过程进行动态仿真。不仅要实现功率输出最大化，还应该尽可能减小风机相关部件的载荷[1-3]。

 

　　因此，本文通过对大型变速变桨距风力发电机组动态特性的分析，提出一种以获取最大能量转换效率为目的的控制算法，该算法能同时兼顾到控制过程良好的动态特性与稳定性，并将机组结构在自然风作用下引起的动力学问题及其疲劳影响程度降到最低。

 

 

　　1.1 风力发电机组动态特性分析

 

　　风力发电机组的动态特性是构成机组各部件的动态特性的总和，它包括风轮的空气动力学特性和结构动力学特性、传动链动态特性、发电机动态特性及控制系统动态特性，如图1所示。

 

　　已设计定型的风力发电机组，其动态特性是确定的，即对于任何给定的输入，它有一个确定的输出响应。如果输入是恒定的，我们可以通过设计，使得系统具有最佳输出；如果输入是变化的，我们希望系统能根据变化来进行适当的调整，使系统保持最佳输出。控制系统的目的就是尽量保持系统的输出在所期望的范围之内。
 

 

　　图1 风力发电机组的动态特性

 

　　1.2 模型线性化

 

　　风力发电机组是一个非线性的复杂系统，直接采用其非线性模型进行控制设计，有较大的难度，控制效果会不太理想。因此，控制算法实现的起点是建立风机动态特性的线性化模型[4]，在此基础上再评估设计的控制算法的性能和稳定性。通常，在应用于实际风电机组之前，控制器要进行三维湍流风输入的仿真验证。当变速变桨距风力发电机组在额定风速以下运行时，通过PI控制器得到给定转矩便可实现平滑控制，转矩控制器的线性化模型也比较简单。必须包括传动链的旋转动态特性，其他动态特性可以忽略。对于变桨控制器的线性化模型，至少应包括以下动态特性：转子和发电机的旋转、塔筒的前后振动、速度传感器响应、变桨执行机构响应等。

 

　　BLADED是广泛应用于风电行业的专业设计软件，具有非常强大的计算和仿真功能。其中，软件的模态线性化模块使用了叶片和塔架结构动力学的模态表示法，能有效建立风力发电机组动态数学模型。因此，利用BLADED软件可以进行模型线性化计算[5]，具体的参数设置如下图所示。
 

 

　　a 模态分析参数

 

 

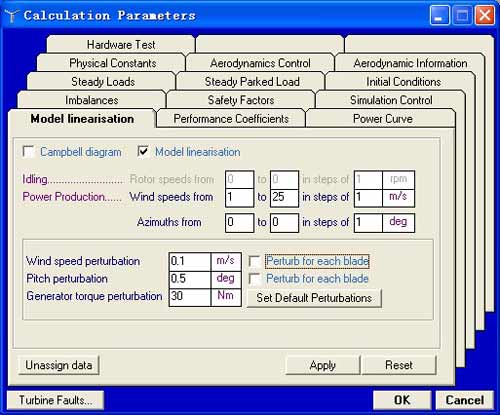
　　b 模型线性化计算参数

 

　　图2 模型线性化参数设置

 

　　从图2中可以看出，模态分析参数主要是选择风轮、塔架等部件模态。对于风轮模态，主要是考虑所用摆振和挥舞的模态数量，一般平面外模态最多6个，平面内模态最多5个。另外，风轮模态还需要考虑桨距角数量和大小，桨距角可以自由设置，一般是选择4个。对于塔架模态，需要考虑前后和左右模态数量，通常是各取2个，至于风轮方位角的选择，可忽略不计。模型线性化计算参数主要是设置风速运行点和风轮方位角运行点，风速扰动、桨距角扰动和发电机转矩扰动等是通过点击Set default perturbations获取。

 

　　1.3 控制模型生成

 

　　模型线性化计算完成后，利用BLADED提供的后处理功能，可将计算结果转化为状态空间模型，其格式为mat文件，这种形式的多输入多输出系统可以直接在MATLAB下进行分析，便于风电机组控制算法的设计。

 

　　状态空间模型[6]不仅能反映系统内部状态，而且能揭示系统内部状态与外部的输入和输出变量的联系，还可以将多个变量时间序列处理为向量时间序列，这种从变量到向量的转变更适合解决多输入输出变量情况下的建模问题。状态空间表达式可以完整描述控制系统的全部信息，其向量矩阵形式如下：

 

　　

 

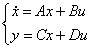
　　式中， 是输入向量， 是系统状态向量， 是输出向量， 为状态矩阵， 为输入矩阵， 为输出矩阵， 为直接转移矩阵。实际上，状态空间表达式就是由状态方程和输出方程构成。利用如下所述的函数可将状态空间方程矩阵转化为风机控制系统的线性时不变数学模型。

 

　　

 

　　式中，SYSTURB.A、SYSTURB.B、SYSTURB.C和SYSTURB.D表示不同运行点的状态空间矩阵，SYSTURB.inputname和SYSTURB.outputname分别表示控制系统模型的输入变量名称和输出变量名称，SYSTURB.statename代表控制系统的状态变量名称。在BLADED中，系统的输入变量有3个：风速、发电机转矩给定和桨距角给定，这是软件设置好的，不可更改。而系统的输出变量则可以根据算法设计需求自行定义。状态变量代表风机各部件机械状态的响应，具体的数量取决于各部件模态选择，数量越多则表示系统考虑的动态特性越多。

 

 

　　2.1 风力发电机组功率特性

 

　　风力发电的能量转换过程包含两部分，先是由风能转换到机械能，然后再从机械能到电能。风力发电机组风轮叶片在自然风作用下产生推力驱动风轮旋转，通过轮毅将扭矩输送到传动链系统，发电机再利用电磁感应原理将传动链系统获得的机械能转换成电能。通常，风机从风能捕获到的机械能功率可表示为[7]：
 

 

 

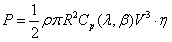
　　式中， 为空气密度； 为风轮半径；为轮毂高度处风速；为风轮的转速；为机组的发电效率，主要是考虑机械损耗和电气损耗后的机组发电效率。为风机的功率系数，表示风机从自然风能中吸取能量的大小程度，与叶片气动性能相关，是叶尖速比和桨距角的函数[7]。在不同桨距角下的曲线如下图所示。

 

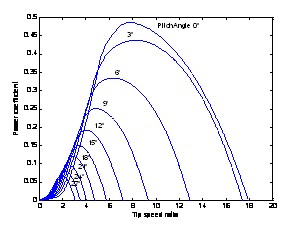
　　图3 风机功率系数曲线

 

　　从图3中可以看出，当桨距角往顺桨位置变化时，风机的功率系数会慢慢减小；当桨距角保持不变时，在最佳叶尖速比处，风力发电机组的风能利用率最高。因此，当风速变化时，只需调节风轮旋转角速度，使其叶尖角速度与风速之比保持不变，就可追踪最佳叶尖速比，继而获得最大功率系数[8]。这就是变速风力发电机组进行转速控制的基本目标。

 

　　2.2 变速变桨距风力发电机组运行区域

 

　　根据风速的大小，大型变速变桨距风力发电机组的运行范围可分为额定风速以下和额定风速以上两个部分。具体的运行区域[9]划分如下图所示。

 

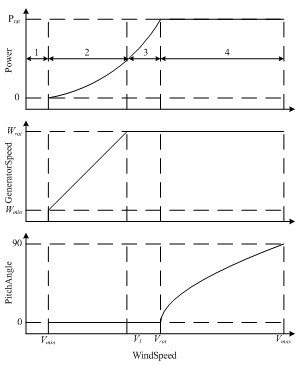
　　图4 变速变桨距风力发电机组运行区域

 

　　由图4可知，在额定风速以下，风机的控制过程又可分为三个不同的阶段：第一阶段是启动阶段(区域1)，机组在风力作用下作机械转动，发电机转速在逐渐增加，可以一直提升到切入转速；第二阶段是变速阶段(区域2)，机组开始获得能量并转换成电能，根据风速的变化调节发电机转速，保持最佳叶尖速比以获得最大风能；第三阶段是恒转速阶段(区域3)，机组通过调节变速电机的转矩从而控制风轮转速保持不变。在额定风速以上，机组进入变桨距控制(区域4)，通过驱动叶片和轮毅之间的齿轮传动机构(即变桨执行机构)来使叶片的攻角随着风速的改变而改变，确保叶片在不同风况下都处于最佳攻角，使得输出功率在额定功率附近保持微小变动。

 

 

　　风力发电机组控制系统的基本目标主要有三个层次：保证风力发电机组安全可靠运行，获取最大能量，提供良好的电能质量。控制算法的设计也是以这三个目标位准则。

 

　　3.1 风力发电机组基本控制策略

 

　　风电机组变速运行，是通过控制发电机输出转矩来实现的。转矩控制器在发电机气隙中产生一个期望

 

　　输出的转矩，引导风机加速或减速，从而使风轮运行在设定的转速附近。为了使气隙中的给定转矩能在很短的时间内达到，控制器的设计需要有较高的带宽。图5所示为转矩控制器所采用的转速-转矩运行曲线。

 

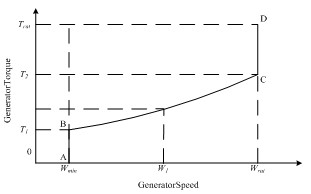
　　图5 变速变桨距风力发电机组转速-转矩运行曲线

 

　　从图5中可看出，在较低风速时(图中BC段)，通过控制发电机的输出转矩来控制风轮转速，以使风电机组实现最大能量捕获；为了降低噪声污染，风机在额定风速到达以前就已经提升到额定转速(C点)，这时通过动态地调整给定转矩，以保持风轮转速稳定在额定值；在风速很低的时候(图中AB段)，也是改变发电机转矩输出值，控制风轮转速保持在最低运行转速；在高风速时，发电机给定转矩达到额定值(D点)，这时需要对桨距角进行控制，通过改变叶片攻角来调整能量的吸收，从而控制风轮转速。在额定点附近，转矩给定值会根据转速的变化作小幅调整，与转速变化成反比，以保持输出功率恒定在额定值。

 

　　当风机达到额定转速后，转矩PI控制器根据发电机转速设定值与实际反馈值的偏差改变给定转矩，使转速不再增加。风轮转速在额定点附近可以有一定的波动，其目的是为了增加传动系统的柔性，使得转矩和功率在额定点附近变化相对平稳。转矩PI控制器的拉普拉斯形式如下：
 

 

　　式中， Kq是比例常数， 是积分时间常数，积分增益是 Kq/Tq 。

 

　　当发电机转矩达到额定值，变桨距控制器就要开始工作。变桨距PI控制器根据发电机的转速反馈，确定桨距角的给定值，以维持转速在设定点。其拉普拉斯形式如下：

 

　　

 

　　式中， K是比例增益， Ti是积分时间常数， G(β)是增益系数。变桨距PI控制器的增益要根据工作点的变化而变化，因为气动力矩对桨距角变化的灵敏度不是线性的，在高风速时要远远高于额定风速时的灵敏度[10]。因此，需要设置桨距角的增益表来实现PI控制器增益跟随工作点变化。通过对增益的调整可以保证变桨距控制器在额定风速到切出风速范围内都具有良好的动态响应和稳定裕度。

 

　　3.2 状态空间模型最小实现

 

　　系统最小实现是一种非常重要的实现方式，属于现代控制理论中的概念[11]。由于单个系统可以写成多个不同状态空间表达形式(即实现)，而如果系统的实现既可控又可观测，则称为系统的最小实现。所以，既可控又可观的系统的实现就是最小实现。不过，最小实现并不是唯一的。

 

　　利用MATLAB控制系统工具箱提供的minreal()函数可以直接求出给定状态空间模型的最小实现，该函数的调用形式为[12]：

 

　　

 

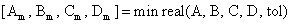
　　其中A，B，C，D为系统模型的状态方程矩阵，tol为用户任意指定的误差限制，如果省略此参数，则默认为最小值(eps)。调用此函数后，就会自动地返回一个最小实现的状态方程模型Am，Bm，Cm，Dm。

 

　　然后再调用其他相关函数，就可构建系统的开环和闭环传递函数，对转矩及变桨距控制器参数进行整定。

 

 

　　本文研究对象为某公司设计的双馈型风电机组模型。其额定功率为1.5MW，发电机额定转速为1770 r/min，外部载荷仿真运行环境选择20 m/s的湍流风，其变化规律如下图所示。
 

 

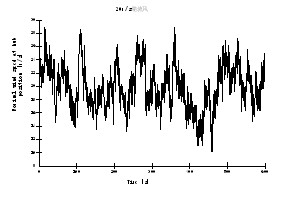
　　图6 20m/s湍流风

 

　　4.1 算法实现

 

 

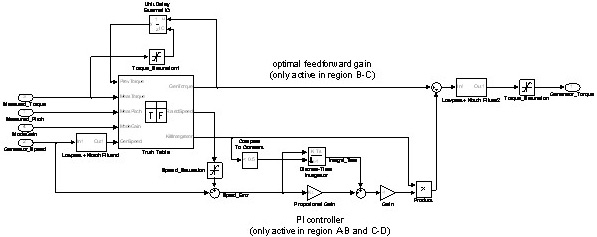
　　图7 转矩控制器

　　图8 变桨距控制器

 

　　根据前面介绍的基本控制策略，利用MATLAB /Simulink中的仿真模块实现风电机组的控制算法设计。MATLAB软件拥有强大的数值计算功能，利用VC与MATLAB接口可以充分发挥其数值计算功能，把复杂的数据处理交给MATLAB去完成，并且可以不依赖MATLAB软件运行。还可利用MATLAB自带的编译工具将mdl文件方便的编译成动态连接库文件(dll)，并可直接供BLADED软件调用。转矩控制器和变桨距控制器的基本框图分别如图7、8所示。

 

　　在图7中可看出，风力发电机组运行区域的判断是通过真值表来完成的，根据电机转速、电机转矩和桨距角三者之间的逻辑关系就可以区分出。转速-转矩运行曲线中的AB段和CD段都是利用转矩PI控

 

　　制器来调整转矩给定，从而控制风轮转速保持在期望值，BC段是使用最优模态增益获得转矩给定值，实现风机的变速运行。

 

　　由图8中可知，变桨控制器是否执行变桨控制也是根据电机转速、电机转矩和桨距角三者之间的逻辑关系，利用真值表实现的。变桨距PI控制器的增益表是通过把MATLAB中拟合好的离散数据导入到Simulink中的查找表，这样就可使得增益系数 根据桨距角的变化而变化。

 

　　4.2 载荷仿真

 

　　BLADED软件外部控制器模块能使用任何期望的控制算法，因此为验证本文所设计控制算法的性能，将对新控制算法与在VC下开发的常规控制算法进行载荷仿真比较，运行风况为如图6所示，下图所示为两种控制算法仿真效果对比。

 

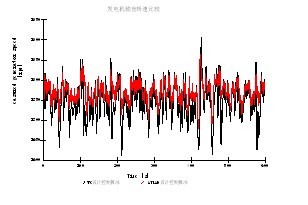
　　图9 发电机输出转速比较

　　图10 发电机输出转矩比较

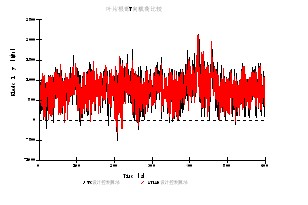
　　图11 叶片根部Y向载荷比较

 

　　在20m/s湍流风条件下，本文所述的控制算法与常规控制算法仿真运行结果比较，发电机输出转速的波动减轻，输出转矩的变化也更平稳，且叶片根部Y方向所受力矩的波动也减小。对于提高风力发电机组的稳定性、可靠性等起到关键的作用，延长了风机的使用寿命，增加了风电场的运行收益。

 

 

　　控制算法的基本目标是保证风电机组的安全运行，获取最大能量转换效率，但同时还须兼顾到控制过程良好的动态特性与稳定性，并将结构在风力作用下引起的动力学问题所产生的疲劳影响减小到最低限度。因此，本文从风机的动态特性分析开始，先讨论基本工作原理，并对变速变桨风力发电机组各风速段的运行特性进行实验研究。在控制算法的实现过程中，应用MATLAB和BLADED软件对完整的控制算法进行了仿真研究，验证了算法的可行性与有效性。

 

　　参 考 文 献

 

　　[1] Thomas Ackermann, Lennart soder. Wind energy technology and current status: a review. Renewable and Sustainable Energy Reviews, 2000, (4):314-374.

 

　　[2] G.M.Joselin Herbert, S.Iniyan, E.Sreevalsan and S.Rajapandian. A review of wind energy technologies. Renewable and Sustainable Energy Reviews, Volume 11, Issue 6, August 2007:1117-1145.

 

　　[3] 叶杭冶. 风力发电机组的控制技术[M]. 北京:机械工业出版社, 2006.

 

　　[4] 李晶,宋家骅,王伟胜.大型变速恒频风力发电机组建模与仿真[J].中国电机工程学报,2004,24(6):100-105.

 

　　LI Jing, SONG Jiahua, WANG Weisheng. Modeling and dynamic simulation of variable speed wind turbine with large capacity[J].Proceeding of the CSEE,2004,24(6):100 -105.

 

　　[5] E.A.Bossanyi. GH Bladed user’s manual. Garrad Hassan &Partners Limited, 2005.

 

　　[6] 包能胜,叶枝全.水平轴风力机状态空间模型参数辨识[J].太阳能学报,2003,24 (3):371-375.

 

　　BAO Nengsheng, YE Zhiquan. State Space Parameter Identification of The Horizontal Wind Turbine System [J]. Acta Energiae Solaris Sinica, 2003,24(3): 371- 375..

 

　　[7] 白焰,范晓旭,吕跃刚,徐大平,杨锡运.大型风力发电机组动态最优控制策略研究[J].电力系统自动化, 2010,34(12): 90-94.

 

　　BAI Yan, FAN Xiaoxu, LV Yuegang, XU Daping, YANG Xiyun.A Study on Dynamic Optimal Control Strategy for Large-scale Wind Power Generation System[J].Automation of Electric Power Systems,2010,34(12):90-94.

 

　　[8] 刘其辉,贺益康,赵仁德.交流励磁变速恒频风力发电系统的运行与控制[J].电工技术学报,2008,23 (01):129-136.

 

　　LIU Qihui, HE Yikang, ZHAO Rende. Operation and Control of AC-Exited Variable-Speed Constantl-Frequency Wind Power Generation System[J].Transactions of China Electrotechnical Society, 2008, 23(1):129-136.

 

　　[9] 刘军,何玉林,李俊,黄文.变速变桨距风力发电机组控制策略改进与仿真[J].电力系统自动化,2011,35(5):82-86.

 

　　LIU Jun, HE Yulin, LI Jun, HUANG Wen. Design and Simulation of an Improved Control Strategy for Variable-speed Pitch Controlled Wind Turbine Driven Generator System[J].Automation of Electric Power Systems, 2011, 35(5):82-86.

 

　　[10] T. Burton, D. Sharpe, N. Jenkins, E. Bossanyi. Wind Energy -Handbook [M]. New York: ASME PRESS, 1994

 

　　[11] 刘豹.现代控制理论.2版[M].北京:机械工业出版社,2000.

 

　　[12] 薛定宇. 控制系统计算机辅助:MATLAB语言及应用[M]. 北京:清华大学出版社, 1996.