首页 > 新闻 > 行业 > 正文
风能资源和风电场开发（三）——风的描述
发布时间：2014-03-06     来源： 《风力发电技术与风电场工程》
本文摘要：　　风能资源和风电场开发（三）——风的描述　　1 风速　　(1) 风速的定义　　通常用风速来表示风的大小，风速是指风的移动速度，即在单
　　风能资源和风电场开发（三）——风的描述
　　1 风速
 
　　(1) 风速的定义
 
　　通常用风速来表示风的大小，风速是指风的移动速度，即在单位时间内空气在水平方向移动的距离，用V表示，单位是m/s，即每秒移动的距离(米)。
 
　　气象学上对风速还给出如下定义：
 
　　1)平均风速，相应于有限时段内的风速的平均值，通常指二分钟或十分钟的平均值，用表示，表1给出了不同时距平均风速近似换算的关系供参考。
 
　　2)瞬时风速：相应于无限小时段内的风速。
 
　　3)最大风速：在给定的时间段或某个期间里面，平均风速中的最大值。
 
　　4)极大风速：在给定的时间段内，瞬时风速的最大值。
 
　　国际上大多数国家采用的风速数据主要是10分钟平均数据，如果风速的平均周期不一致，相应的风速结果也会不同。
 
　　风速是一个随机性很大的物理量，随时间和季节频繁变化，甚至瞬息万变。利用测风设备测得的风速是在一个极短时间段内得到的数值。要想得到平均风速，就要在一定的时间段内多次测量，然后计算其平均值。测风时取空间某一点，将某一个测风周期的平均风速如小时平均风速、月平均风速、年平均风速等为测风周期内各次观测风速之和除以观测次数，得到：

 
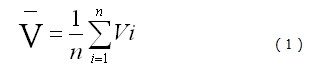
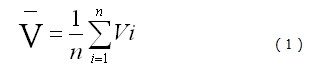
　　式中为平均风速：Vi为时间点i对应的瞬时风速；n为平均风速计算时段内(年、月或日)所选取样本点的总数。
 
　　(2) 风速的分布
 
　　目前比较常用的分析风速分布的方法是将风速值离散化，把不同风速值划分到相应的风速段(如4.6～5.5m/s之间的风速划分到5m/s，其他风速依此类推)，将风速的间隔定为1m/s，计算一年周期中不同平均风速累计小时数，绘制成概率密度曲线图。
 
　　通常用于拟合风速分布的函数很多，有瑞利分布、对数正态分布、威布尔分布等。风速分布一般为偏正态分布，一般用威布尔分布函数来描述风速分布的概率密度函数：
 
　　f(V) = K/C(V/C)K-1exp[-(V/C)]K      (2)
 
　　式中C为尺度系数，单位为m/s，C与平均风速相关，平均风速越大，C值越大；K为形状系数，反映风速的分布情况，K值越大，说明风速分布越集中，K值越小，说明风速分布越分散；
 
　　但需要指出的是存在威布尔拟合与实际分布差别较大的情况，有些地区的风速分布可能并不服从威布尔分布，在这种情况下可以对分析结果进行修正或采用其他的分析方法。
 
　　图1是2套测风数据进行威布尔拟合的曲线图，纵坐标表示风速频率f(%)，横坐标表示风速大小u(m/s)，可以看出，左图比右图更接近威布尔分布。
 
　　(3) 平均风速随时间变化
 
　　1)日变化：风在一日内有规律的周期变化。平均风速日变化的原因主要是太阳辐射的日变化而造成地面热力不均匀。日出后，地面热力不均匀性渐趋明显，地面温度高于空气温度，气流上、下发生对流，进行动量交换，上层动量向下传递，使上层风速减小，下层风速增加。入夜后，则相反。在高、低层中间则有一个过渡层，那里风速变化不明显，一般过渡层在50m～150m高度范围。平均风速日变化在夏季无云时较强，而在冬季多云时则偏弱。
 
　　2)月变化：一般指一年时段中以月为单位的逐月风速的周期变化。有些地区，在一个月中，有时会发生周期为一天或几天的平均风速变化，其原因是热带气旋和热带波动的影响所造成的。
 
　　3)季变化：一年中以季为单位的风速的季节变化。平均风速随季度变化的大小取决于纬度和地貌特征，通常在北半球中高纬度大陆地区，由于冬季有利于高压生成，夏季有利于低压生成，因此，冬季平均风速要大一些，夏季平均风速要小一些。我国大部分地区，最大风速多在春季的三、四月，而最小风速则多在夏季的七、八月。
 
　　4)年变化：常指风速在一年内的变化。
 
　　5)年际变化：风速月或年平均在不同年之间的变化。从而了解它的变化大小，趋势等。
 
　　2 风向
 
　　(1) 风向的定义
 
　　风向：风的来向。风向表示方法有：度数表示法和方位表示法。
 
　　度数表示法是最直接的风向表示方法，用0～360°度数表示风的来向，这种表示方法通俗简单。为了更加直观的表示风的来向，采用方位表示，就是把0～360°的风向离散化，把不同风向值划分到相应的扇区，如图3所示，通常设16扇区，每隔22.5度为一个扇区，如348.75～360°和0～11.25°区间的风向为北风，以N表示，11.25～33.75°区间的风向为北东北风，以NNE表示，33.75～56.25°区间的风向为东北风，以NE表示，其他的依次类推。
 
　　(2) 风向、风能的分布
 
　　目前比较常用的分析统计风向分布特点的方法是将测风周期所测的风向值离散化，把不同风向值划分到相应的扇区，然后分析在测风时间内风向在不同扇区出现的频率，从而判断风向分布状况。用同样的方法可以判断风能的分布情况。测风周期通常取1月或1年。
 
　　一般采用风向和风能玫瑰图来描述风向、风能在水平面上的分布情况。所谓的玫瑰图是根据风向或风能在各扇区的频率分布，以相应的比例长度绘制的形如玫瑰花朵的概率分布图。
 
　　需要指出的是当主风向和主风能的方向不一致时，应以风能玫瑰图为主。也就是说，在一个测风周期内风向出现的频率高，对应的风能不一定多，因为风能与风速的立方成正比，风速比风频对主风能方向的影响更明显。
 
　　图4表示的是某测风塔风向、风能分布玫瑰图，从风向玫瑰图来看，南风出现的频率最高，其次为西西北和西北风，从风能玫瑰图来看，西北方向风能频率最高，其次为西西北和南风，综合来看，测风塔的主风向为西北和西西北风。这是因为南风虽然出现的频率较高，但风速较小，对应的风能不大，而西北风出现的频率虽然相对较小，但风速较大，对应的风能较大，为最大风能方向。
 
　　3 风能和风功率密度
 
　　(1) 风能
 
　　风能是大气运动具有的动能，在单位时间内流过某一截面的风能E，亦即风功率的计算公式为：
 
　　E=0.5ρSV3 (3)
 
　　式中：E：风能，单位为W；
 
　　Ρ：空气密度，单位为kg/m3；
 
　　S：气流通过的截面积，单位为m2，
 
　　V：风速，单位为m/s。
 
　　风能的大小分别与空气密度、通过的截面积以及气流速度的立方成正比。
 
　　(2) 风功率密度
 
　　风功率密度是气流在单位时间垂直通过单位面积的风能：
 
　　P=0.5ρV3 (4)
 
　　式中：P：风功能密度，单位为W/m2；
 
　　ρ：空气密度，单位为kg/m3；
 
　　V：风速，单位为m/s。
 
　　风功率密度的大小与空气密度、气流速度的立方成正比。
 
　　在风能和风功率密度计算中，最重要的因素是风速，风速增加1倍，风能或风功率密度增加7倍。
 
 
　　一般来讲，年平均风速越大，年平均风功率密度也越大，风能可利用的小时数也越多，风电场发电量越高。因此，年平均风速和风功率密度是评价风电场风能资源水平的主要指标。随着风力发电机组技术的提高、轮毂高度的增加以及造价的降低，一般风功率密度等级达到2级，风电场就具备开发价值。
 
　　4 空气密度
 
　　空气密度是指单位体积的空气质量。
 
　　在标准大气压下，15℃时的每立方米空气重量为1.225kg。
 
　　空气密度的计算式1：

 
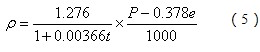
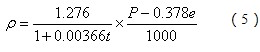
　　式中：Ρ：平均空气密度，kg/m3；
 
　　p：平均气压，hPa；
 
　　e：平均水汽压，hPa；
 
　　t：平均气温为，℃。
 
　　空气密度的计算式2：

 
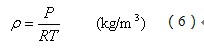
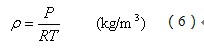
　　式中：P：年平均大气压力，Pa；
 
　　R：气体常数(287 J/kg˙K)；
 
　　T：年平均空气开氏温标绝对温度(℃+273)。
 
　　空气密度的计算式3：
 
　　ρ=(353.05/T)exp-0.034(z/T) (kg/m3) (7)
 
　　式中：z：海拔高度，m；
 
　　T：年平均空气开氏温标绝对温度(℃ + 273)。
 
　　5 粗糙度和风切变指数
 
　　(1) 粗糙度
 
　　由于地面对风的摩擦力，风速随离地面高度而发生显著变化。风廓线是表示风速随离地面高度变化的曲线。
 
　　粗糙度即粗糙长度，它是衡量地面对风的摩擦力大小的指标，在假定垂直风廓线随离地面高度按对数关系变化情况下，平均风速变为0时算出的高度。一般来讲，地表表面的粗糙度越大，对风的减速效果越明显。例如，森林和城市对风速影响很大，草地和灌木地带对风的影响相对比较大，机场跑道对风的影响相对较小，而水面对风的影响更小。
 
　　(2) 对数分布律
 
　　在近地层，风速随离地面高度有显著变化。造成风在近地层中的垂直变化的原因有动力因素和热力因素，前者主要来源于地面的摩擦效应，即地面的粗糙度，后者主要表现与近地层大气垂直稳定度的关系。在离地高度100m内的近地层中，可以忽略剪切应力的变化，这时，风廓线可采用普朗特(Prandtl)对数率分布来表示：

 
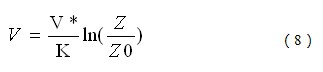
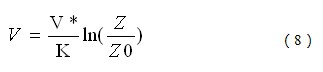
　　式中：V-高度Z 处的风速，m/s；
 
　　V*-摩擦速度，m/s；
 
　　K-卡门常数，其值为0.4左右；
 
　　Z0-粗糙度，m；
 
　　Z-离地高度，m。
 
　　(3) 指数分布律
 
　　用指数律分布计算风廓线比较简便，一般情况下，风速随高度变化可以用幂指数公式来描述：

 
　　式中：Vn和V0-距地面高度Hn和H0处的风速，单位分别为m/s 和m；
 
　　α-风切变指数，是衡量风速随高度变化快慢的指标。
 
　　风切变，又称风切或风剪，它反映了风速随着高度变化而变化的情况，包括气流运动速度的突然变化、气流运动方向的突然变化。
 
　　风切变指数对于风电机组的设计非常重要，同一台风力发电机在不同的高度，获得的风能是不同的。例如，一台风力发电机的轮毂高度为40m，叶轮直径为40m，则叶轮扫风面最上端(60m高度)的风速可达9.3m/s，最下端(20m高度)的风速为7.7m/s，这就意味着叶轮扫风面承受巨大的压力差。
 
　　根据风电机组的设计规范，风电机组轮毂高度处的风切变系数不高于0.2。
 
　　距离地面1000m以上的风况几乎不受地面的影响，但是在大气层的近地面层，风速受到地面摩擦的影响较大。图5—图7分别表示出不同粗糙度情况下的风廓线比较图、风从平滑地表吹向粗糙地表时的风廓线变化图和风从粗糙地表吹向平滑地表时的风廓线变化图。
 
　　6 湍流强度
 
　　在近地层中，气流具有明显的湍流特征，湍流是一种不规则随机流动，其速度有快速的大幅度起伏，并随时间、空间位置而变。
 
　　湍流强度是衡量气流脉动强弱的相对指标，常用标准差和平均速度的比值来表示。在图1-8中，在平均风速相同的条件下，右侧风速的湍流强度大于左侧湍流强度。
 
　　湍流强度会减小风力发电机组的风能利用率，同时也会增加机组的疲劳载荷和机件磨损几率。在风电机组的设计规范中，对风电机组所承受的不同湍流强度做了规定。一般情况下，可以通过增加风力发电机组的轮毂高度来减小由地面粗糙度引起的湍流强度的影响。
 
　　(选自《风力发电技术与风电场工程》杨校生主编出版社：化学工业出版社 )


 
关键词：风能 电场 资源

【收藏】【打印】【关闭】【返回顶部】

分享到：
相关文章